|
|
Full
transformation semigroups have very regular holonomy decompositions,
that can be quite misleading when someone tries to say something about
the general case.
Generators:
x = (2 3 4 5 1), y=(2 2 3 4 5), z=(2 1 3 4 5)
(Generators are in transformation notation,
but only the bottom line is displayed. This is not the cyclic notation
for permutations.)
Decomposition:
(2,S2) wr (3,S3) wr (4,S4) wr (5,S5)
(underscore means that constant maps are included, Sn is the symmetric group on n points)
Tiling picture:
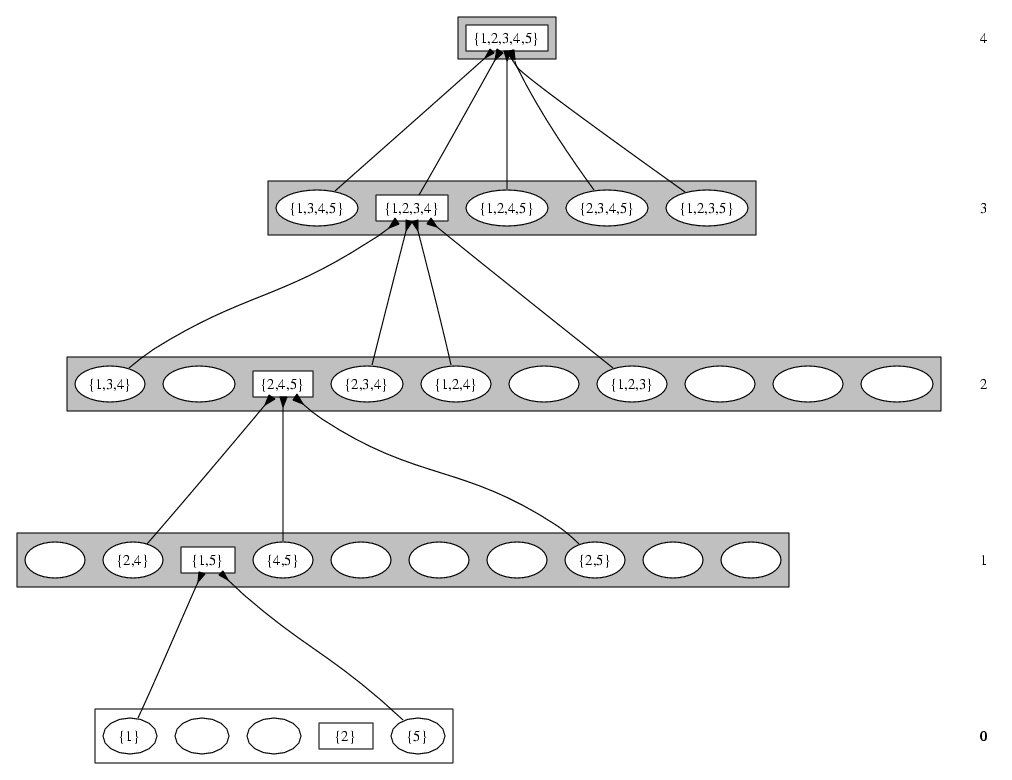
(The arrows with plugs denote the tile of
relation. Numbers on the right denote the hierarchical levels. Nodes
are the elements of the extended set of images. Boxes denote subduction
equivalence classes. Rectangular nodes are arbitrary chosen class
representatives.)
Poset of equivalence class representatives:
BACK
|
|
|